ตามนิยามของความเร่ง ซึ่งคือการเปลี่ยนความเร็วต่อเวลา ความเร่งเฉลี่ยย่อมเขียนเป็นสัญลักษณ์ตามสมการต่อไปนี้ คือ
หากเป็นความเร่งเฉลี่ยระหว่างจุด P และ Q ความเร็ว ![]() และ
และ ![]() คือความเร็ว (ขณะใดขณะหนึ่ง) ที่จุด Q และ P ตามลำดับ
คือความเร็ว (ขณะใดขณะหนึ่ง) ที่จุด Q และ P ตามลำดับ ![]() ต้องเป็นการลบอย่างเวกเตอร์ นั่นคือ
ต้องเป็นการลบอย่างเวกเตอร์ นั่นคือ ![]() อาจมีขนาดและทิศเป็นไปตามรูปใดรูปหนึ่งของรูป 2.7
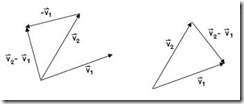
อาจมีขนาดและทิศเป็นไปตามรูปใดรูปหนึ่งของรูป 2.7
รูป 2.7 การลบอย่างเวกเตอร์แสดงความเร็วที่เปลี่ยนไปในช่วงเวลาที่กำหนด
ขนาดและทิศของความเร็วที่เปลี่ยนไปในช่วงเวลา ![]() แสดงด้วยเวกเตอร์
แสดงด้วยเวกเตอร์ ![]() และเมื่อจุด P และ Q เข้าใกล้กันมากๆ ความเร่งเฉลี่ยกลายเป็นความเร่งขณะใดขณะหนึ่งได้โดย
และเมื่อจุด P และ Q เข้าใกล้กันมากๆ ความเร่งเฉลี่ยกลายเป็นความเร่งขณะใดขณะหนึ่งได้โดย ![]() ตามสัญลักษณ์ของแคลคูลัส มีความหมายดังได้กล่าวมาแล้วดังรูป 2.6 ความเร็วที่เปลี่ยนไปไม่จำเป็นต้องอยู่ในทิศของความเร็วเดิม ซึ่งหมายความว่าความเร่งของการเคลื่อนที่ไม่จำเป็นต้องอยู่ในทิศเดียวกับความเร็ว จะเป็นที่ขณะใดๆ ก็ตาม
ตามสัญลักษณ์ของแคลคูลัส มีความหมายดังได้กล่าวมาแล้วดังรูป 2.6 ความเร็วที่เปลี่ยนไปไม่จำเป็นต้องอยู่ในทิศของความเร็วเดิม ซึ่งหมายความว่าความเร่งของการเคลื่อนที่ไม่จำเป็นต้องอยู่ในทิศเดียวกับความเร็ว จะเป็นที่ขณะใดๆ ก็ตาม
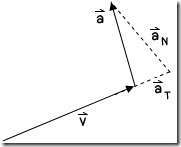
แผนภาพเชิงเวกเตอร์ของความเร่งเทียบกับเวกเตอร์ความเร็วที่ขณะหนึ่ง อาจเป็นดังรูป 2.7 ซึ่งโดยทั่วไปความเร่งอาจทำมุมขนาดหนึ่งที่ไม่ตั้งฉากกับความเร็วดังรูป และสามารถจะมองได้ว่า มีองค์ประกอบหนึ่งของความเร่งที่ตั้งฉากกับความเร็ว สมมุติให้เป็น ![]() และมีอีกองค์ประกอบหนึ่งอยู่ในแนวของความเร็วให้เป็น
และมีอีกองค์ประกอบหนึ่งอยู่ในแนวของความเร็วให้เป็น ![]() ทั้งสององค์ประกอบแสดงไว้ในรูป 2.8
ทั้งสององค์ประกอบแสดงไว้ในรูป 2.8
รูป 2.8 แผนภาพเชิงเวกเตอร์ของความเร็วและความเร่ง