การเคลื่อนที่ในกรณีความเร่งเป็นค่าคงตัว
กรณีที่ความเร่งมีค่าคงตัว (Constant acceleration) นั่นคือ ความเร็วมีการเปลี่ยนแปลง
แบบสม่ำเสมอ กราฟของความเร็วที่เพิ่มขึ้นอย่างสม่ำเสมออาจเป็นดังรูป ซึ่งกราฟความเร็วกับ เวลาเป็นกราฟเส้นตรง ความชันที่ทุกจุดบนเส้นตรงคือ ความชันของเส้นตรงนั่นเอง
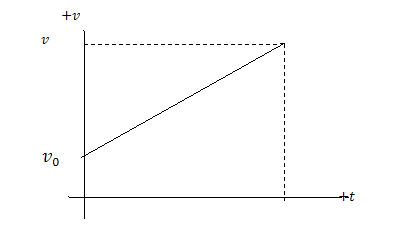
รูป กราฟความเร็วกับเวลา
ความชันของเส้นตรงคือ 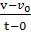 ให้เท่ากับ ให้เท่ากับ 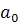 ซึ่งเป็นค่าคงตัว ซึ่งเป็นค่าคงตัว
ดังนั้น 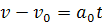
หรือ 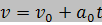
ความหมายในสมการนี้คือ 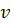 เป็นความเร็วที่เวลา เป็นความเร็วที่เวลา 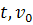 เป็นความเร็วที่เวลา เป็นความเร็วที่เวลา
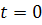 หรือความเร็วต้น , หรือความเร็วต้น , 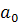 เป็นความเร่งค่าหนึ่ง และ เป็นความเร่งค่าหนึ่ง และ 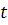 เป็นเวลา ซึ่งจากสมการ เป็นเวลา ซึ่งจากสมการ
ข้างต้นก็จะเห็นได้ว่า ความเร็วมีค่าเพิ่มขึ้นอย่างสม่ำเสมอ สมการนี้จะใช้ได้ทั้งค่า
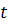 ที่เป็น + และ – (ค่า – ที่เป็น + และ – (ค่า – 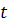 หมายถึงเวลาก่อนที่จะเริ่มนับว่าศูนย์) และยังใช้ได้ทั้ง หมายถึงเวลาก่อนที่จะเริ่มนับว่าศูนย์) และยังใช้ได้ทั้ง
กรณีที่ 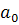 เป็นบวกและลบ (ถ้า เป็นบวกและลบ (ถ้า 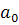 มีค่าเป็นลบ หมายถึงความเร่งไปทางทิศ –X และ มีผลให้ความเร็ว ลดลงอย่างสม่ำเสมอ โดยที่ มีค่าเป็นลบ หมายถึงความเร่งไปทางทิศ –X และ มีผลให้ความเร็ว ลดลงอย่างสม่ำเสมอ โดยที่ 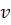 อาจจะยังมีค่าเป็นบวกอยู่) อาจจะยังมีค่าเป็นบวกอยู่)

รูป กราฟระหว่างความเร็วและเวลา สำหรับความเร่งคงตัว
การหาระยะทางที่วัตถุเคลื่อนที่ได้ อาจจะหาได้โดยใช้กราฟดังรูป 2.5 ถ้าใช้ช่วง
เวลา 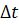 เป็นช่วงเวลาสั้น ๆ ขณะที่วัตถุมีความเร็ว เป็นช่วงเวลาสั้น ๆ ขณะที่วัตถุมีความเร็ว 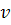 ระยะทางที่วัตถุเคลื่อนที่ได้ในช่วง ระยะทางที่วัตถุเคลื่อนที่ได้ในช่วง
เวลา  ก็คือ ก็คือ 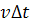 ซึ่งเป็นช่วงเวลาสั้น ๆ เปลี่ยนแปลงไม่มาก ดังนั้นการรวม ซึ่งเป็นช่วงเวลาสั้น ๆ เปลี่ยนแปลงไม่มาก ดังนั้นการรวม 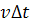
ทั้งหมดโดยเริ่มจาก 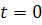 จนถึง จนถึง 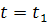 จะได้ระยะทางของการเคลื่อนที่ทั้งหมด และเป็นระยะ ทางที่ถูกต้อง เมื่อ จะได้ระยะทางของการเคลื่อนที่ทั้งหมด และเป็นระยะ ทางที่ถูกต้อง เมื่อ 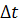 เข้าใกล้ศูนย์ นั้นคือ การอินทิเกรต (integrate) ของ เข้าใกล้ศูนย์ นั้นคือ การอินทิเกรต (integrate) ของ 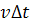 จาก จาก 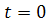 จนถึง จนถึง  จะให้ระยะทางทั้งหมดสมมติว่าเป็น จะให้ระยะทางทั้งหมดสมมติว่าเป็น 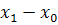 โดยสัญลักษณ์คือ โดยสัญลักษณ์คือ
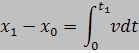
ตามรูป 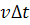 เป็นพื้นที่ใต้กราฟที่สูง เป็นพื้นที่ใต้กราฟที่สูง 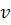 และกว้าง และกว้าง 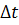 การรวมพื้นที่ การรวมพื้นที่ 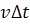 ทั้งหมดจะได้พื้นที่ ใต้กราฟทั้งหมดเป็นรูปสี่เหลี่ยมคางหมูที่มีด้านขนานสูง ทั้งหมดจะได้พื้นที่ ใต้กราฟทั้งหมดเป็นรูปสี่เหลี่ยมคางหมูที่มีด้านขนานสูง 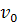 กับ กับ 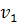 มีความกว้าง มีความกว้าง 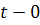
ซึ่งมีค่าเท่ากับ 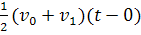 นั่นคือ นั่นคือ 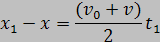
และเมื่อแทนค่า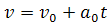 จะได้ จะได้ 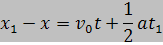 ขณะที่ ขณะที่
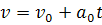 ดังนั้น ดังนั้น 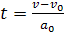 แทนค่าใน แทนค่าใน 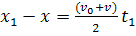 จะได้ จะได้
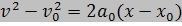
ดังนั้นสูตรจะเป็นดังนี้
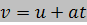
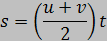
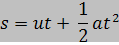
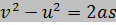
สูตรเหล่านี้ใช้ได้เฉพาะกรณีที่ a เป็นค่าคงตัวเท่านั้น |