นิวตันเสนอกฎแรงดึงดูดระหว่างมวลไว้ว่า
วัตถุทั่งหลายในเอกภพจะออกแรงดึงดูดซึ่งกันและกัน โดยขนาดของแรงดึงดูดระหว่างวัตถุคู่หนึ่ง ๆจะแปรผันตรงกับผลคูณระหว่างมาลวัตถุที่สองและจะแปรผกผันกับกำลังสองชองระยะทางระหว่างวัตถุทั้งสองนั่น”
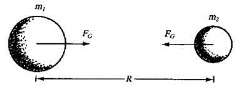
ตามกฎแรงดึงดูดระหว่างมวลที่นิวตันเสนอ พิจารณาจากรูป เราจะสามารถเขียนได้ว่า
เมื่อ m1 และ m2 เป็นมวลของวัตถุแต่ละก้อน มีหน่วยเป็น กิโลกรัม
R เป็นระยะระหว่างมวล m1 กับm2 มีหน่วยเป็น เมตร
G เป็นค่าคงตัวความโน้มถ่วงสากล เท่ากับ 6.673 x10-11 นิวตัน – เมตรต่อกิโลกรัม2
FG เป็นแรงดึงดูดระหว่างมวล m1 กับm2 มีหน่วยเป็น นิวตัน
แรง FG ตามกฎของนิวตันมีความหมายว่า เป็นแรงดูดอย่างเดียวไม่มีแรงผลัก และเป็นแรงกระทำร่วม กล่าวคือมวล m1 และ m2 ต่างฝ่ายต่างดูดซึ่งกันcละกันด้วยแรงขนาด ตามสมการ (1 )แต่ทิศทางตรงข้ามกัน ไม่มีใครดูดใครมากกว่าใคร
มวลของโลก
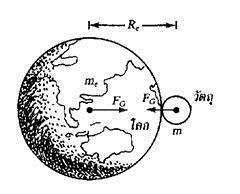
จากรูป วัตถุมวล m อยู่ที่ผิวโลกซึ่งมีมวล me มีรัศมี Re วัตถุและโลกต่างดูดซึ่งกันและกันด้วยแรง Fe มีค่าเป็น
แรงที่วัตถุและโลกต่างดูดซึ่งกันและกันนี้แท้จริงคือน้ำหนักของวัตถุนั่นเอง ดังนั้นถ้า g เป็นอัตราเร่งโน้มถ่วงที่ผิวโลกจากสมการ (2) จะเขียนใหม่ได้เป็น
สมการ 4 เป็นสมการที่แสดงค่ามวลของโลก ซึ่วถ้าทราบรัศมีของโลกเราจะสามารถคำนวณมวลของโลกได้สมมติถ้ารัศมีของลกเท่ากับ 6.38 x106 เมตร จะได้มวลของโลก meเท่ากับ
ในการพิจารณามวลของโลก เราจะไม่ได้สมการ(4) ถ้าเราตัดมวล m ทั้งสองข้างจะได้
จากสมการ (6) จะเห็นว่า ค่า g ซึ่งเป็นค่าความเร่งเนื่องจากแรงโน้มถ่วง จะมีค่าขึ้นกับรัศมีโลก Re หรืออาจกล่าวให้ชัดเจนขึ้นว่า g ขึ้นกับระยะทางห่างจากโลกออกไป กล่าวคือ g จากเมื่อระยะทางน้อย และ g จะน้อยเมื่อระยะทางงมาก หรือกล่าวสรุปว่า g แปรผันกับระยะห่างจากจุดศูนย์กลางของโลกยกกำลังสอง
ความเร่งเนื่องจากแรงโน้มถ่วง ณ ตำแหน่งลึกลงไปใต้ผิวโลก
ในกรณีที่พิจารณา g ที่ตำแหน่งลึกลงไปใต้ผิวโลกจะพบว่า g แปรผันโดยตรงกับระยะจากศูนย์กลางของโลกถึงตำแหน่งที่พิจารณา และมีค่าเป็นศูนย์ที่จุดศูนย์กลางของโลก โดยจะได้
g = (4/3)G p rR ………….(7)
เมื่อ r เป็นความหนาแน่นของโลก และ R เป็นระยะจากศูนย์กลางโลกถึงตำแหน่งที่พิจารณา